Digital control system

Digital Control Systems Analysis and Design

homework

1.아래의 sampled-data closed-loop system에서 입력신호가 unit step function이고 sample time이 0.1sec일때 k번째 샘플타임의 y(k)식을 유도하시오.
2.그리고 p,i,d 제어기를 추가하여 delay time이 감소하도록 설계해보시오. 먼저 pip를 활용하여 control module을 다운받는다.

pip install control

그리고 그래프를 확인하기 위해 matplotlib과 numpy, control 모듈들을 import한다
(numpy는 왜 import 했을까?? 항상 그래프를 그릴때 np를 활용해서 그려서 습관적으로 넣은것 같긴 하다)

import numpy as np
import matplotlib.pyplot as plt
import control

이번에 하는 시스템의 경우에는 이산시간 시스템이기 때문에 sample time을 설정 해 주어야 한다

Ts=0.1
z=control.TransferFunction.z

시스템을 동작시키기 전에 과제에서 주어진 신호를 생성한다
시스템은 PD제어기로 주어졌으며 sample time은 0.1초이다
그리고 제시된 루프의 경우에는 feedback loop이므로 control module에서 feedback loop를 사용한다
여기서 print함수를 사용하면 우리가 수식으로 편하게 표현하는 형식으로 볼 수 있다
여기서 내가 zero-hold마저 자연스럽게 laplace에서 z-domain으로 변경하면 좋겠지만 아직 방법을 찾지 못해서 (절대 과제제출하고 끝나서 그런건 아니다) 부득이 하게 손으로 z변환 한 다음에 함수로 표현하게 되었다
자연스럽게 numpy도 활용하였다

Rz=control.tf([1,0],[1,-1],Ts)
Mz=control.tf([3, -1],[1,0],Ts)
Gz=control.tf([1-np.exp(-3*Ts)],[3,-3*np.exp(-3*Ts)],Ts)
tf=control.feedback(Gz*Mz,1)
Yz=tf*Rz
print(Yz)

위에 보면 특이사항없이 전부 출력이 되었다. 우리가 구하고자 하는것은 1번 문제의 k번째의 y(k)값을 구하고 싶으므로 z-domain에 있는것을 다시 time domain으로 바꾸어준다. ~하지만 패키지 내에서 찾지 못해서 실패~

여기가 내가 생각하는 핵심 부분인데 control.step_responese를 활용하여 시스템에 u(t)가 입력이 되었을때 시스템을 확인 할 수 있다.
우선 위에서 제시된 system의 그래프를 그려보면

tz, yz =control.step_response(tf)
plt.plot(tz, yz)
plt.grid()

위와 같이 그래프가 나오게 된다. 여기서 그래프를 그릴때 Yz가 아닌 tf가 들어간 이유는 함수 이름 자체가 control.step_response이기 때문에 입력값인 r(t)는 따로 추가하지는 않는다.
기존에 제시된 함수 자제가 PI제어기였으므로 I제어기 먼저 확인해 보면 아래와 같은 그래프가 나오게 된다.

mz_1=control.tf([Ts],[1,-1],Ts)
tf_1=control.feedback(mz_1*Gz,1)
tz1,yz1=control.step_response(tf_1)
plt.plot(tz1,yz1, label='Backward')

mz_2=control.tf([Ts,0],[1,-1],Ts)
tf_2=control.feedback(mz_2*Gz,1)
tz2,yz2=control.step_response(tf_2)
plt.plot(tz2,yz2,label='Forward')

mz_3=control.tf([Ts,Ts],[1,-1],Ts)
tf_3=control.feedback(mz_3*Gz,1)
tz3,yz3=control.step_response(tf_3)
plt.plot(tz3,yz3, label='Trapezoid')

plt.legend()
plt.grid()

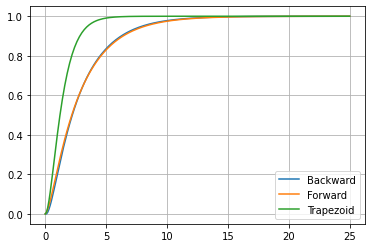
위에 그래프는 I제어기들의 세가지 형식을 모두 표현한 것이다
backward는 후향구형적분, forward는 전향구형적분, Trapezoid는 사다리꼴적분이고 각각의 rising time을 비교해 볼 수 있다.

mz_4=control.tf([1,-1],[Ts,0],Ts)*Ts
tf_4=control.feedback(mz_4*Gz,1)
tz4,yz4=control.step_response(tf_4)
plt.plot(tz4,yz4, label='Derivative')

D제어기의 경우 미분값을 이용하므로 미분값이 커지거나 작아지면 미리 컨트롤 하기 때문에 PD제어기를 사용하지 않으면 위와 같이 0수렴하게 된다. P제어기의 값에 의해 PD제어기도 overdump가 발생할수도 있고 안할수도 있다.

P1=2
mz_5=control.tf([1,-1],[1,0],Ts)+P1
tf_5=control.feedback(mz_5*Gz,1)
tz5,yz5=control.step_response(tf_5)
plt.plot(tz5,yz5, label='P=2')

P2=6
mz_6=control.tf([1,-1],[1,0],Ts)+P2
tf_6=control.feedback(mz_6*Gz,1)
tz6,yz6=control.step_response(tf_6)
plt.plot(tz6,yz6, label='P=6')

P3=10
mz_7=control.tf([1,-1],[1,0],Ts)+P3
tf_7=control.feedback(mz_7*Gz,1)
tz7,yz7=control.step_response(tf_7)
plt.plot(tz7,yz7, label='P=10')

plt.grid()
plt.legend()

위에서 p값들을 변경해가면서 overdump가 발생하는지 안하는지 확인을 해 보았다 이건 교수님께서 수업하시면서 정확한 P값을 구하는것을 알려주시진 않고 경험적으로 표현하신다고 하였으므로 나도 이정도로 정리한다